CS 280A HW2 Report

1.1: Finite Difference Operator

To obtain the difference between adjacent pixels of an image $\mathbf{I}$$\bold I$, we can define filters $\begin{array}{c}{\mathbf{D}}_{\mathbf{x}}=[1,-1],{\mathbf{D}}_{\mathbf{y}}=\left[\begin{array}{c}1\\ -1\end{array}\right]\end{array}$$\bold D_\bold x=[1,\ -1],\ \bold D_\bold y=\begin{bmatrix*}1\\-1\end{bmatrix*}$ to compute the gradient in $x$$x$-direction and $y$$y$-direction by convoluting them with the origin image.

$\mathbf{I}\ast {\mathbf{D}}_{\mathbf{x}}$$\bold I * \bold D_\bold x$	$\mathbf{I}\ast {\mathbf{D}}_{\mathbf{y}}$$\bold I * \bold D_\bold y$

Note that the range of the convoluted image's pixels are $[-1,1]$$[-1,\ 1]$, I normalized them by the function $f(x)=\frac{x+1}{2}$$f(x) = \frac{x+1}{2}$ for better visualizations.

Next, the gradient magnitude image ${\mathbf{I}}_{\text{grad}}$$\bold I_{\text {grad}}$ can be computed by ${\mathbf{I}}_{\text{grad}}=\sqrt{(\mathbf{I}\ast {\mathbf{D}}_{\mathbf{x}}{)}^2+(\mathbf{I}\ast {\mathbf{D}}_{\mathbf{y}}{)}^2}$$\bold I_{\text{grad}} = \sqrt{(\bold I*\bold D_\bold x)^2 + (\bold I*\bold D_\bold y)^2}$, where the $\ast$$*$ operation denotes the convolution. Lastly, by applying binary-thresholding process, we can get the binarized edge image $I_{\text{bin}}$$I_{\text{bin}}$, which showed the pixels with a larger gradient.

${\mathbf{I}}_{\text{grad}}$$\bold I_{\text{grad}}$	${\mathbf{I}}_{\text{bin}}$$\bold I_\text{bin}$

1.2: Derivative of Gaussian Filter

To remove noises generated by the lawn in the image, I convoluted the original image $\mathbf{I}$$\bold I$ with a Gaussian filter $\mathbf{G}$$\bold G$ to create a blurred image ${\mathbf{I}}^{\prime }=\mathbf{I}\ast \mathbf{G}$$\bold I' = \bold I*\bold G$. Similarly, we can compute ${\mathbf{I}}_{\text{grad}}^{\prime }$$\bold I'_{\text{grad}}$ and ${\mathbf{I}}_{\text{bin}}^{\prime }$$\bold I'_{\text{bin}}$ by the method mentioned in section 1.1.

${\mathbf{I}}^{\prime }\ast {\mathbf{D}}_{\mathbf{x}}$$\bold I' * \bold D_\bold x$	${\mathbf{I}}^{\prime }\ast {\mathbf{D}}_{\mathbf{y}}$$\bold I' * \bold D_\bold y$
${\mathbf{I}}_{\text{grad}}^{\prime }$$\bold I'_{\text{grad}}$	${\mathbf{I}}_{\text{bin}}^{\prime }$$\bold I'_{\text{bin}}$

By applying Gaussian blur to the image, I saw the difference that the noises generated by the lawn are suppressed. This is mainly because the areas of the gradients generated by lawn are small. Therefore, they can be smoothed by the Gaussian blur and not be considered an "edge."

Notice that ${\mathbf{I}}_{\text{grad}}^{\prime }=\sqrt{({\mathbf{I}}^{\prime }\ast {\mathbf{D}}_{\mathbf{x}}{)}^2+({\mathbf{I}}^{\prime }\ast {\mathbf{D}}_{\mathbf{y}}{)}^2}=\sqrt{(\mathbf{I}\ast \mathbf{G}\ast {\mathbf{D}}_{\mathbf{x}}{)}^2+(\mathbf{I}\ast \mathbf{G}\ast {\mathbf{D}}_{\mathbf{y}}{)}^2}$$\bold I'_{\text{grad}} = \sqrt{(\bold I' * \bold D_\bold x)^2+(\bold I'*\bold D_\bold y)^2} = \sqrt{(\bold I*\bold G * \bold D_\bold x)^2+(\bold I*\bold G * \bold D_\bold y)^2}$, since convolution is associative, we can compute $\mathbf{G}\ast {\mathbf{D}}_{\mathbf{x}}$$\bold G * \bold D_\bold x$ and $\mathbf{G}\ast {\mathbf{D}}_{\mathbf{y}}$$\bold G * \bold D_\bold y$ first. In this assignment, it is called Derivative of Gaussian (DoG) filter.

Now, compute ${\mathbf{I}}_{\text{grad}}^{\prime }$$\bold I'_{\text{grad}}$ by $\mathbf{DoG}$$\bold{DoG}$: ${\mathbf{I}}_{\text{grad}}^{\prime }=\sqrt{(\mathbf{I}\ast {\mathbf{DoG}}_x{)}^2+(\mathbf{I}\ast {\mathbf{DoG}}_y{)}^2}$$\bold I'_{\text{grad}}=\sqrt{(\bold I * \bold{DoG}_ x)^2 + (\bold I * \bold{DoG}_y)^2}$.

$\bold I * \bold{DoG}_\bold x$	$\mathbf{I}\ast {\mathbf{DoG}}_{\mathbf{y}}$$\bold I * \bold{DoG}_\bold y$
${\mathbf{I}}_{\text{grad}}^{\prime }$$\bold I'_{\text{grad}}$ (by DoG filter)	${\mathbf{I}}_{\text{bin}}^{\prime }$$\bold I'_{\text{bin}}$ (by DoG filter)

Now we verified that ${\mathbf{I}}_{\text{bin}}^{\prime }$$\bold I'_{\text{bin}}$ obtained from two different methods are essentially the same.

2.1: Image "Sharpening"

Based on the fact that the Gaussian filter behaves like a low-pass filter, we can obtain the high frequencies ${\mathbf{I}}_{\text{hf}}$$\bold I_{\text{hf}}$ of an image by subtraction.

Since ${\mathbf{I}}_{\text{hf}}$$\bold I_{\text{hf}}$ is the "details" of an image, adding them to the original image yields a "sharpened" image ${\mathbf{I}}_{\text{sharp}}$$\bold I_{\text{sharp}}$.

, where $\alpha$$\alpha$ is the parameter to control the extent of sharpening. $\alpha =0$$\alpha = 0$ keeps the image unchanged.

In the following examples, I chose $\alpha =3$$\alpha = 3$.

	+3$\cdot$$\cdot$		=
	+3$\cdot$$\cdot$		=

I picked an image of Sather Gate. I blurred it first and tried to resharpen it based on the blurred image.

Origin
Blurred
Resharpened

Unfortunately, the resharpen process failed to "restore" the blurred image. The characters on the Sather Gate are still vague after resharpening.

2.2: Hybrid Images

To generate a hybrid image, given two images ${\mathbf{I}}_1,{\mathbf{I}}_2$$\bold I_1,\ \bold I_2$, we can extract the low frequencies of one image and the high frequencies of the other and average them. In my implementation, instead of simply averaging them, I used the weighted average for better visual effects. Formally, it can be expressed as:

, where $a,b$$a,\ b$ are hand-tuned parameters.

For example, take the following images as ${\mathbf{I}}_1,{\mathbf{I}}_2$$\bold I_1,\ \bold I_2$:

${\mathbf{I}}_1$$\bold I_1$ (Frieren)	${\mathbf{I}}_2$$\bold I_2$ (Anya)

I kept the low frequencies of Frieren and the high frequencies of Anya to generate the hybrid image "Frierenya":

"Frierenya"

The image looks more like Frieren when you look far away, while it looks more like Anya when you look close.

Now, let's inspect the frequencies of these images by Fourier analysis.

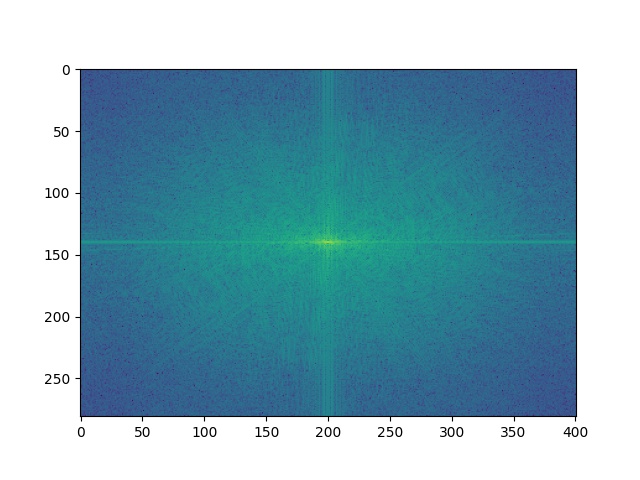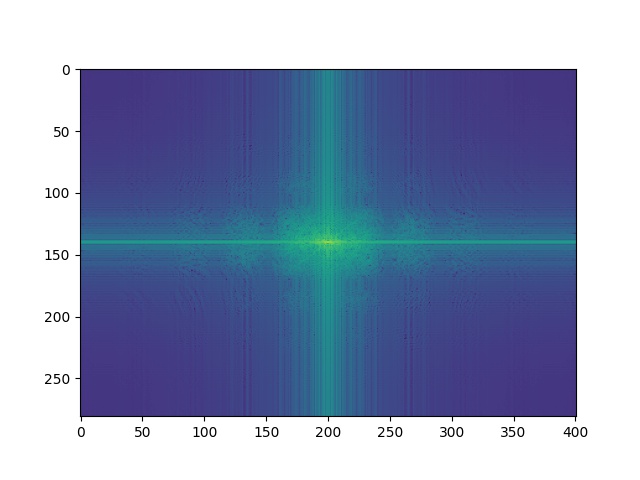Frieren's frequencies	Low frequencies of Frieren
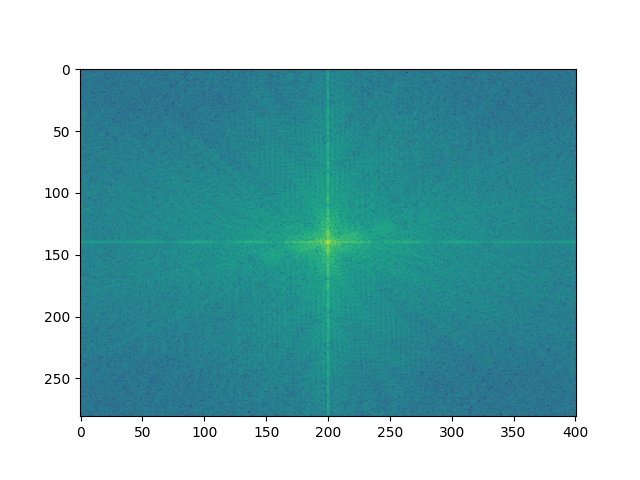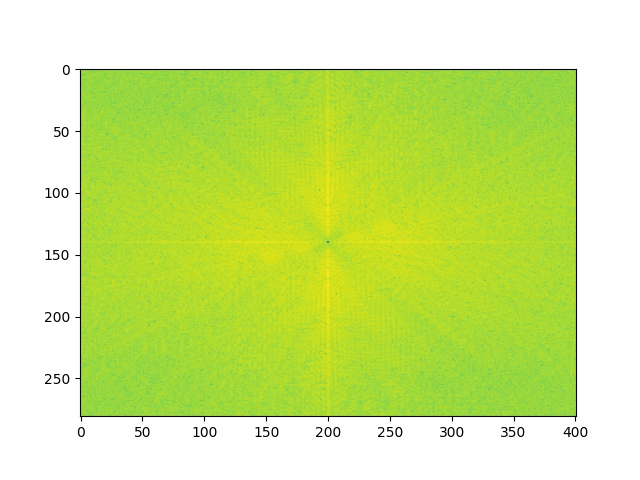Anya's frequencies	High frequencies of Anya

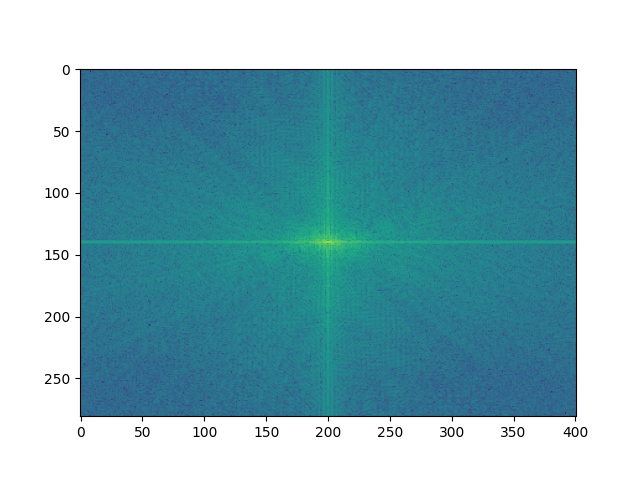Frierenya's frequencies

Similarly, I applied the merge process to two more pairs of images.

${\mathbf{I}}_1$$\bold I_1$ (Albert Einstein)	${\mathbf{I}}_2$$\bold I_2$ (Alexei Efros)

"Albert Efros"

The result seems acceptable, though Prof. Efros' collar aligned with Einstein's chin because of Einstein's large head (note that their eyes are aligned!).

The following is a failed example:

Campanile	Big Ben

"???????"

For me, it seems like some strange texture on the surface of Campanile. I can't discern Big Ben through this image.

2.3: Gaussian and Laplacian Stacks

For the purpose of blending images, we need to compute their Gaussian stack and Laplacian stack first. Let the image be $\mathbf{I}$$\bold I$, the Gaussian stack of $\mathbf{I}$$\bold I$ can be obtained by repeatedly convolute $\mathbf{I}$$\bold I$ with a Gaussian filter $\mathbf{G}$$\bold G$. Therefore, a Gaussian stack of $\mathbf{I}$$\bold I$ with $N$$N$ levels can be expressed as:

, where

In my implementation, the kernel size of the Gaussian filter increased doubly as the level increased by one to capture the image's features in various scales.

The Laplacian stack can be derived from the Gaussian stack. It is defined as:

where

The original image can be constructed by summing up the Laplacian stack.

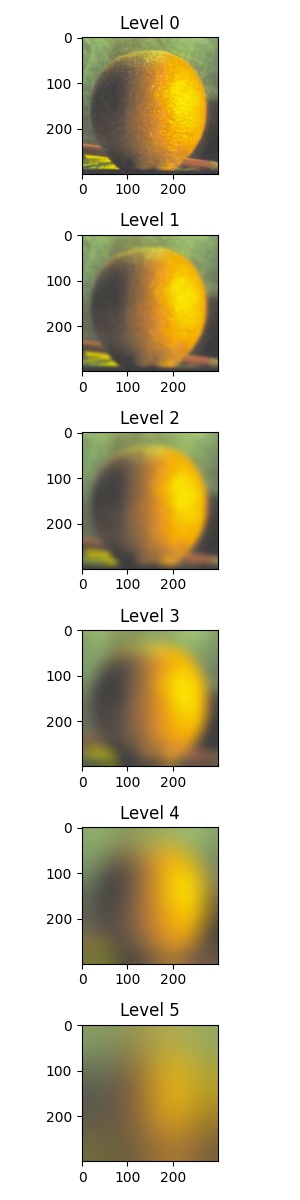
The following are the Laplacian stack examples of an apple and orange:

${\mathbf{I}}_{\mathbf{G}}$$\bold I_\bold G$ for apple	${\mathbf{I}}_{\mathbf{L}}$$\bold I_\bold L$ for apple

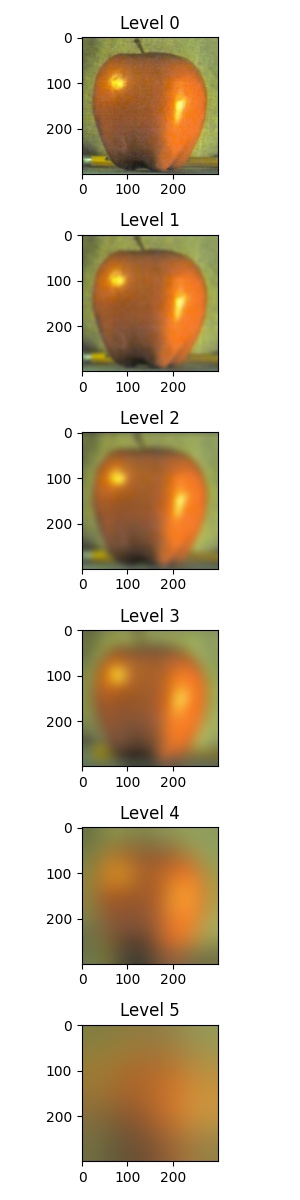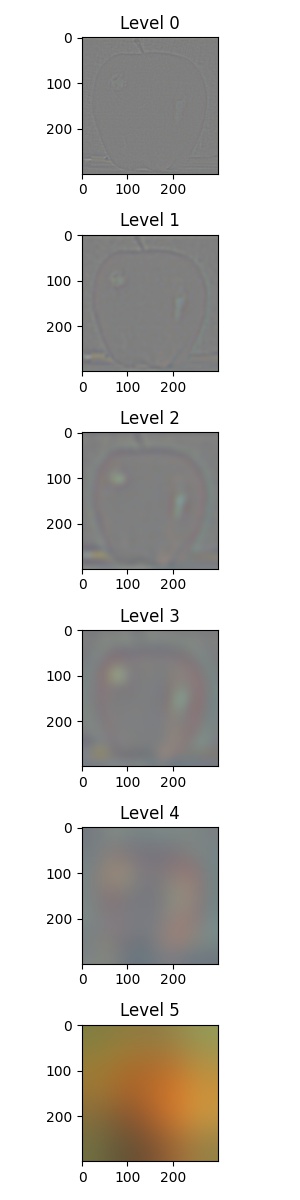For the first five levels of the Laplacian stack (Level 0 ~ Level 4), since the value of each pixel ranged from $[-1,1]$$[-1,\ 1]$, I linearly transformed them into $[0,1]$$[0,\ 1]$ for better visualization (just as the one did in section 1.1).

${\mathbf{I}}_{\mathbf{G}}$$\bold I_\bold G$ for orange	${\mathbf{I}}_{\mathbf{L}}$$\bold I_\bold L$ for orange

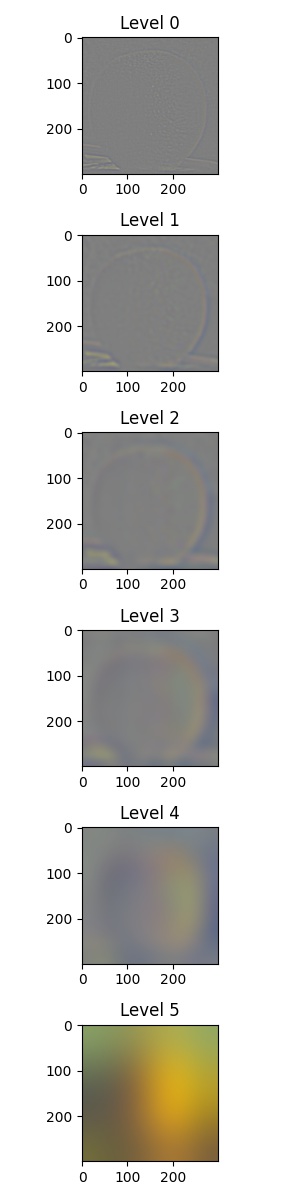We also need a Gaussian stack of a mask to blend two images. In the "oraple" example, a mask that vertically divides the image is needed:

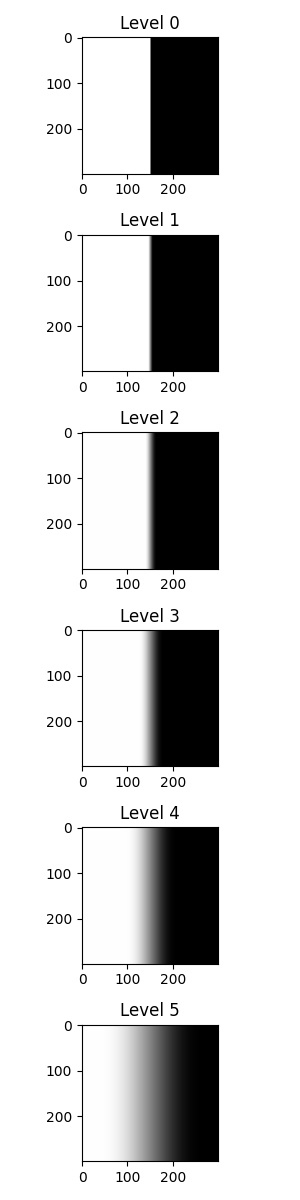
The Laplacian stack of the blended image can be computed by the formula:

, where ${\mathbf{I}}^A$$\bold I^A$ is the blended image, ${\mathbf{I}}^B$$\bold I^B$ and ${\mathbf{I}}^C$$\bold I^C$ are the images to be blended (apple and orange in this example), $\mathbf{M}$$\bold M$ is the mask, and $\times$$\times$ is the element-wise multiplication.

Finally, ${\mathbf{I}}^A$$\bold I^A$ can be constructed by ${\mathbf{I}}_{\mathbf{L}}^A$$\bold I^A_\bold L$ through the formula (1).

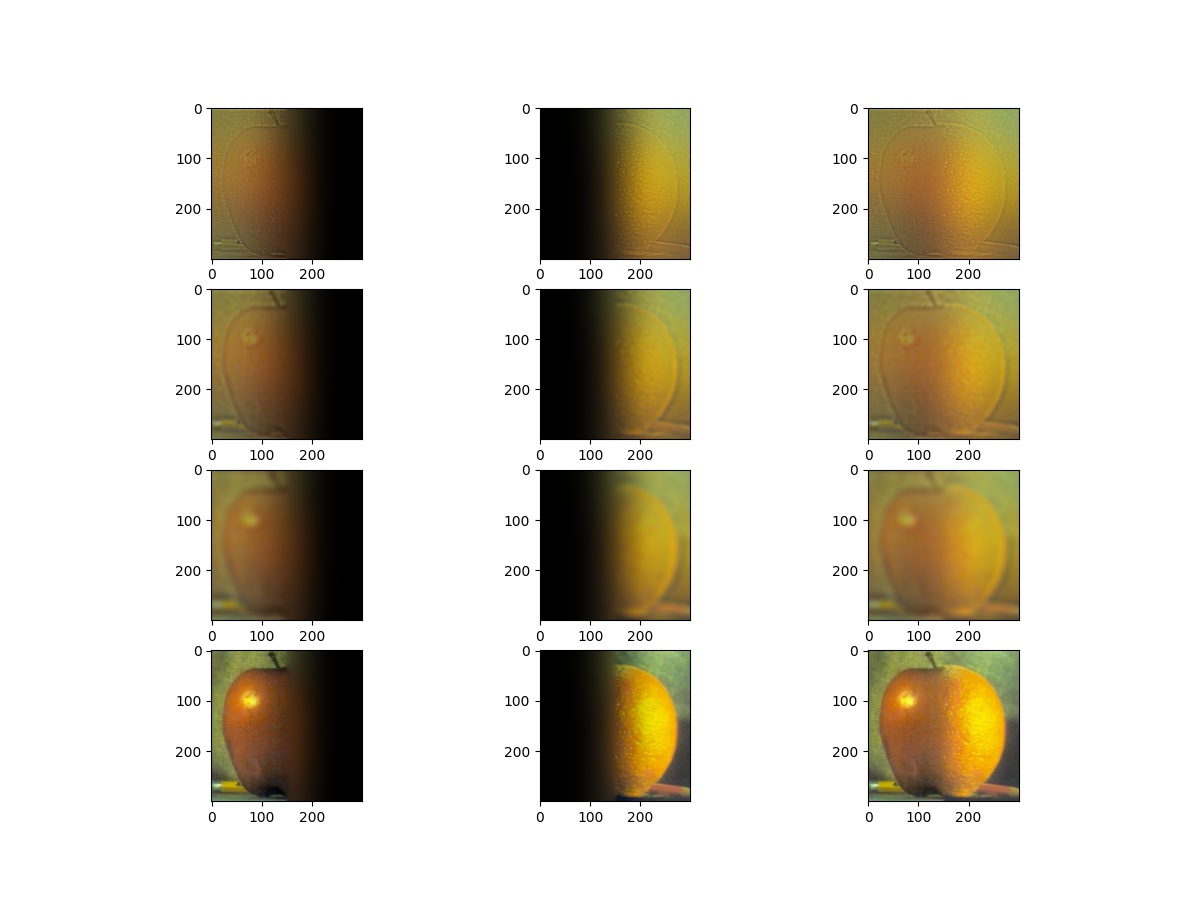Blending process

The first three rows are levels 0, 2, and 4. The last row is the summation of the stack. The columns are the different levels of ${\mathbf{M}}_{\mathbf{G}}\times {\mathbf{I}}_{\mathbf{L}}^B,{\mathbf{M}}_{\mathbf{G}}\times {\mathbf{I}}_{\mathbf{L}}^C$$\bold M_\bold G\times\bold I^B_\bold L, \bold M_\bold G\times\bold I^C_\bold L$, and ${\mathbf{I}}_{\mathbf{L}}^A$$\bold I^A_\bold L$. (apple, orange, oraple)

For better visualization, the images in the last level of the Laplacian stack are added to the images in the first three rows. For instance, the top-left image is ${\mathbf{M}}_{\mathbf{G},0}\times {\mathbf{I}}_{\mathbf{L},0}^B+{\mathbf{M}}_{\mathbf{G},N-1}\times {\mathbf{I}}_{\mathbf{L},N-1}^B$$\bold M_{\bold G, 0}\times \bold I^B_{\bold L, 0} + \bold M_{\bold G, N-1}\times \bold I^B_{\bold L, N-1}$ . I did this because these images look more reasonable than the images normalized by other methods.

The final result is:

2.4: Multiresolution Blending

As described in section 2.3, we can blend arbitrary image pairs with an appropriate mask.

Mr. Bean

Hell Rock's Kitchen

What makes Hell's Kitchen even more intense? Gordon "The Rock" Ramsay!

Sadly, since their poses are not 100% the same, the white part on the right shoulder is hard to remove based on this method.