CS 280A HW1 Report

Problem Formulation

Given three unaligned color channels (RGB) of an image, find a good alignment for them and generate the aligned image.

Problem Example

Given an image like this:

Our goal is to place them together and generate a full-color image:

In contrast, placing them together without any optimization yields:

Method

In this section, we will introduce each procedure of the final algorithm, including:

• Exhaustive search

• Image pyramid

• Match score matrics

  • L2-distance (Euclidean distance)

  • Dot product

  • Canny edge detection

Finally, we will give the full picture of the solution at the end of this section.

Exhaustive Search

Given two unaligned channels, we search over the pre-defined displacement window (in our implementation, it is [-18, 18] pixels,) scoring each displacement with a score matric, which we'll discuss later, and choosing the one with the highest score.

Note that in this procedure, we score the channels for $(18+18+1{)}^2=1369$$(18 + 18 + 1)^2 = 1369$ times. It may be time-consuming for larger images, especially when computing the match score is non-trivial. Another shortcoming of this procedure is that the pre-defined window may not be sufficient for large images. One possible solution to this is to enlarge the pre-defined window size. However, it could significantly increase the computation efforts. Therefore, we need the "image pyramid" to accelerate the process.

Image Pyramid

Image pyramid rescales the original image in multiple sizes and exhaustively searches from the smallest image to the original image. Once we find a displacement on a small image, we can narrow down the search window and apply it to a larger image. The process repeats until we find the displacement on the original image.

In our implementation, we rescale images by a factor of 2, and the smallest rescaled is no larger than 100000 pixels. Formally, for a $m\times n$$m \times n$ image $I_{m\times n}$$I_{m\times n}$, the image pyramid $P$$P$ is defined as:

For convenient nomination, let $I_k$$I_k$ denote $I_{2^{-k}m\times 2^{-k}n}$$I_{2^{-k}m\times2^{-k}n}$. If we find a displacement $(x_k,y_k)$$(x_k, y_k)$ on $I_k$$I_k$, then the displacement on $I_{k-1}$$I_{k-1}$ should be near at $(2\cdot x_k,2\cdot y_k).$$(2\cdot x_k,\ 2\cdot y_k).$ That is, $(x_{k-1},y_{k-1})\approx (2\cdot x_k,2\cdot y_k)$$(x_{k-1},\ y_{k-1}) \approx (2\cdot x_k,\ 2\cdot y_k)$. Therefore, we can conduct an exhaustive search with a small search window at $(x_{k-1},y_{k-1})$$(x_{k-1},\ y_{k-1})$ on $I_{k-1}$$I_{k-1}$.

Match Score Metrics

The next question is, how to define a "good alignment" between two channels? Since the channels were derived from the same image, we assume that a "good alignment" makes the two channels "similar". In this section, we'll introduce two pixel-based metrics (L2-distance and dot product) and one hybrid metric (Canny edge detection).

L2-Distance (Euclidean Distance)

A straightforward intuition for measuring the similarity of two channels $C_1\text{ and }{C}_2$$C_1\text{ and } C_2$ is to compute the Euclidean distance between them. We compute the distance between each pixel from two channels and sum it up. The match score $S_{L2}$$S_{L2}$ is defined as:

Note that we take the negative sign to make sure that the higher score represents the higher similarity.

However, we didn't use Euclidean distance in our final implementation since it doesn't give a favorable result.

Dot Product

Another method is to compute the dot product $v_1\cdot v_2$${v_1\cdot v_2}$, where $v_1$$v_1$ is a flattened vector of $C_1$$C_1$ and $v_2$$v_2$ is a flattened vector of $C_2$$C_2$. The match score $S_{\text{dot}}$$S_{\text{dot}}$ is defined as:

Canny Edge Detection

The above pixel-based metrics assume that in a "good alignment", the value of each corresponding pixel pair shares the same pattern. In Euclidean distance, it assumes the value between two corresponding pixels is close. On the other hand, the dot product score encourages the image that has high values in both pixels in many corresponding pixel pairs. Though, a real-world image doesn't follow this pattern. For instance, a red color pixel has a high value in the red channel and has low values in the rest. The above methods are likely to fail in matching an image with many red pixels.

To solve this problem, we need to find a feature that is consistent in different channels. We assume that object edges can be observed in all channels. Canny edge detection is a popular edge detection algorithm. It starts with Gaussian filter to remove the noise, find the intensity gradients of the image, apply thresholds to determine potential edges, and finally detect edges by hysteresis thresholding. For more information, refer here.

After applying Canny edge detection, it gives a matrix consisting of only $\{0,1\}$$\{0, 1\}$, where $1$$1$ stands for the edges. Then we use the dot product approach mentioned above to score the similarity between two channels. $S_{\text{edge}}$$S_{\text{edge}}$ is defined as:

Method Pseudocode

Our method's pseudocode is presented as follows:

function search_align(c1, c2, search_window, starting_displacement)
  max_score := 0
  best_displacement := (0, 0)
  c1_edge := Canny_edge_detection(c1)
  c2_edge := Canny_edge_detection(c2)
  for displacement in search_window:
    displaced_c1_edge := shift_pixel(c1_edge, starting_displacement + displacement)
    score := dot_product_score(displaced_c1_edge, c2_edge)
    if score > max_score:
      max_score = score
      best_displacement = displacement
  return best_displacement


function pyramid_align(c1, c2):
  if c1.pixel_count < 100000:
    return search_align(c1, c2, big_window, (0, 0))
  scaled_c1 := rescale(c1, 0.5)
  scaled_c2 := rescale(c2, 0.5)
  displacement := pyramid_align(scaled_c1, scaled_c2)
  return search_align(c1, c2, small_window, displacement)


function align_channels(r, g, b):
  aligned_r := pyramid_align(r, b)   % use b channel as reference
  aligned_g := pyramid_align(g, b)
  aligned_image := [aligned_r, aligned_g, b]
  return aligned_image

The aligning process starts with align_channels(), which calls pyramid_align() twice to align three channels. pyramid_align() is a recursive function. Its base case calls a search_align() with a large search window. Its recursive cases rescale the two channels to a smaller size and call itself to obtain the displacement on the smaller channel, then call a search_align() with a small search window. search_align() conducts an exhaustive search over two given channels. It first finds the edges of two channels by the Canny edge detection algorithm, and exhaustively computes the dot product score between two channels in the search window.

Bells & Whistles

Automatic Cropping

We conduct automatic cropping after the aligned image is generated. Since there are borders in aligned images, we use the Canny edge detection algorithm to detect them, and find their exact coordinate by diagonally approaching. That is, we start from the left-top point $(0,0)$$(0, 0)$, and iteratively increase the coordinate to $(1,1),(2,2),(3,3),\dots$$(1, 1),\ (2, 2),\ (3, 3), \dots$ until we reach the border edge. A similar procedure is done on the right-bottom point as well. We then crop the image according to the found left-top point and right-bottom point.

Automatic White Balance

We implement the "grey world" method mentioned in the lecture slide on page 36. We compute the mean value of each channel and linearly scale them to force the mean value to $0.5$$0.5$ . Note that we need to do this after automatic cropping since there are redundant white (or black) borders in the uncropped images.

Result

For each image pair below, the left one is the one without automatic white balance while the right one is the one with automatic white balance.

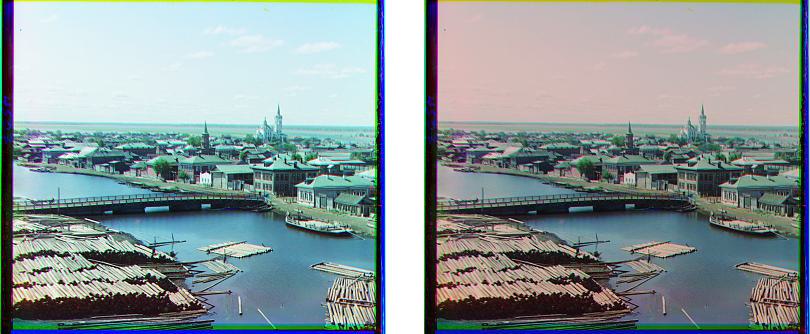
Offset Table

Other Images